Zach’s facts
Zach’s facts have been extracted from the book to remind you of the key concepts you and Zach have learned in each chapter.
Zach's Facts 4.1 Fitting models
- Scientists fit models to the data they observe. These models (hopefully) reflect the true state of the world (i.e., what is happening in the population).
- Models that fit the observed data well are said to have ‘good fit’.
- Bigger samples give us a better idea of what’s happening in the population (i.e., the true state of the world) compared to small samples.
- Most of the models that we use to describe the state of the world can be thought of as variations on this equation:
![]()
Zach's Facts 4.2 Central tendency
- A simple ‘model’ of the real world is one that estimates the ‘typical’ score. There are several ways to do this.
- The mean is the sum of all scores divided by the number of scores. It is the balancing point of the scores; that is, the distances between each score below the mean and the mean are the same (overall) as the distances between each score above the mean and the mean. For this reason, the value of the mean can be influenced quite heavily by extreme scores (scores a long distance from the mean).
- The median is the middle score when the scores are placed in ascending order. It is not as influenced by extreme scores as the mean.
- The mode is the score that occurs most frequently.
Zach's Facts 4.3 Dispersion
- There are several ways to quantify how well the mean ‘fits’ the data. The deviance or error is the distance of each score from the mean.
- The sum of squared errors is the total amount of error in the mean. The errors/deviances are squared before adding them up.
- The variance is the average distance of scores from the mean. It is the sum of squares divided by the number of scores. It tells us about how widely dispersed scores are around the mean, and is also a measure of how well the model ‘fits’ the observed data. If you have all of the population data it can be calculated as:
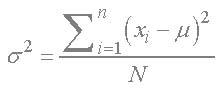
- If you want to estimate the population variance from a sample of data, then use this formula instead:
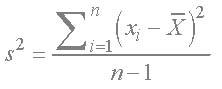
- The standard deviation is the square root of the variance. It is the variance converted back to the original units of measurement of the scores used to compute it. For this reason it is the most commonly cited measure of the ‘fit’ of the mean, or the dispersion of scores around the mean.
- Large standard deviations relative to the mean suggest data are widely spread around the mean (it is a poor ‘fit’); whereas small standard deviations suggest data are closely packed around the mean (it is a good ‘fit’).
- The range is the distance between the highest and lowest score.
- The interquartile range is the range of the middle 50% of the scores.
