Multiple choice questions

Quizzes are available to test your understanding of the key concepts covered in each chapter. Click on the quiz below to get started.

1.    A psychologist was interested in whether the amount of news people watch (minutes per day) predicts how depressed they are (from 0 = not depressed to 7 = very depressed). What does the standardized beta
tell us in the output? 
(Hint: The standardized beta values are measured in standard deviation units.)

Ch 14_Fig 1

  1. As news exposure decreases by 0.224 standard deviations, depression increases by 1 standard deviation.
  2. As news exposure increases by 1 minute, depression decreases by 0.224 units.
  3. As news exposure decreases by 0.224 minutes, depression increases by 1 unit.
  4. As news exposure increases by 1 standard deviation, depression decreases by 0.224 of a standard deviation.

The correct answer is d) As news exposure increases by 1 standard deviation, depression decreases by 0.224 of a standard deviation. This is because the standardized beta values tell us the number of standard deviations by which the outcome will change as a result of one standard deviation change in the predictor. 

2.    A psychologist was interested in whether the amount of news people watch predicts how depressed
they are. Based on the output, is news exposure a significant predictor of depression?

Ch 14_Fig 2

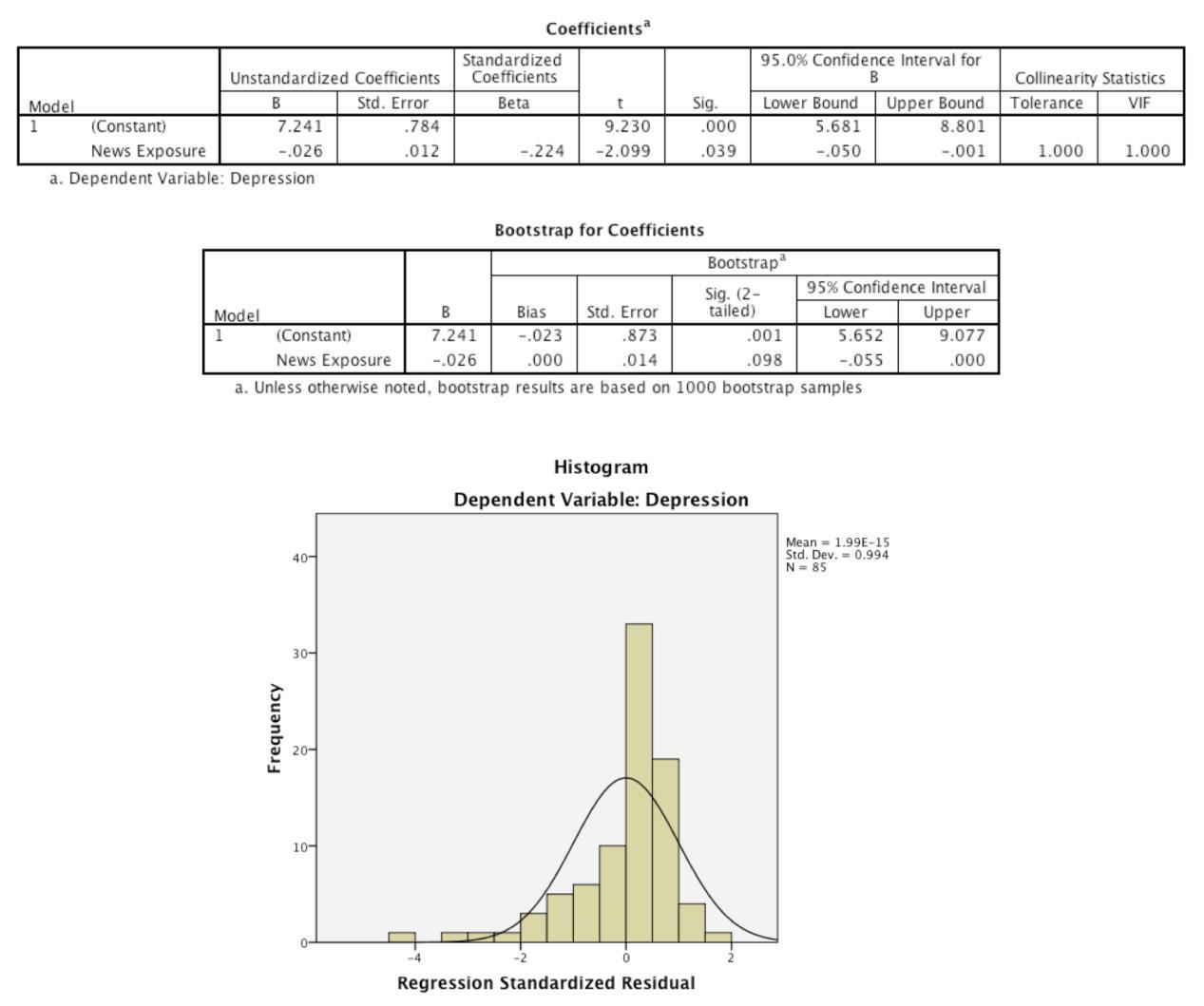
  1. No, because the bootstrap significance value of news exposure is greater than .05. 
  2. Yes, because the p-value for news exposure is .039, which is less than .05. 
  3. Yes, because the bootstrapped confidence interval for news exposure contains zero.
  4. No, because the confidence interval for news exposure does not contain zero.

The correct answer is a) No, because the bootstrap significance value of news exposure is greater than .05.  This is because the histogram shows a non-normal distribution, so we use the bootstrapped estimates. 

3.    A consumer researcher was interested in what factors influence people's fear responses to horror
films. She measured gender (0 = female, 1 = male) and how much a person is prone to believe in things
that are not real (fantasy proneness) on a scale from 0 to 4 (0 = not at all fantasy prone, 4 = very fantasy prone). Fear responses were measured on a scale from 0 (not at all scared) to 15 (the most scared I have ever felt). What is the likely population value of the parameter describing the relationship between gender and fear?

Ch 14_Fig 3

  1. -1.943 
  2. Somewhere between -3.498 and -0.392
  3. Somewhere between -3.369 and -0.517
  4. .008

The correct answer is c) Somewhere between -3.369 and -0.517. This is because the plot does not indicate any assumptions violated, so we can use the regular confidence interval. 

4.    A psychologist was interested in whether the amount of news people watch predicts how depressed
they are. Based on the output below, is there evidence that a meaningful relationship exists in the
population?

Ch 14_Fig 4

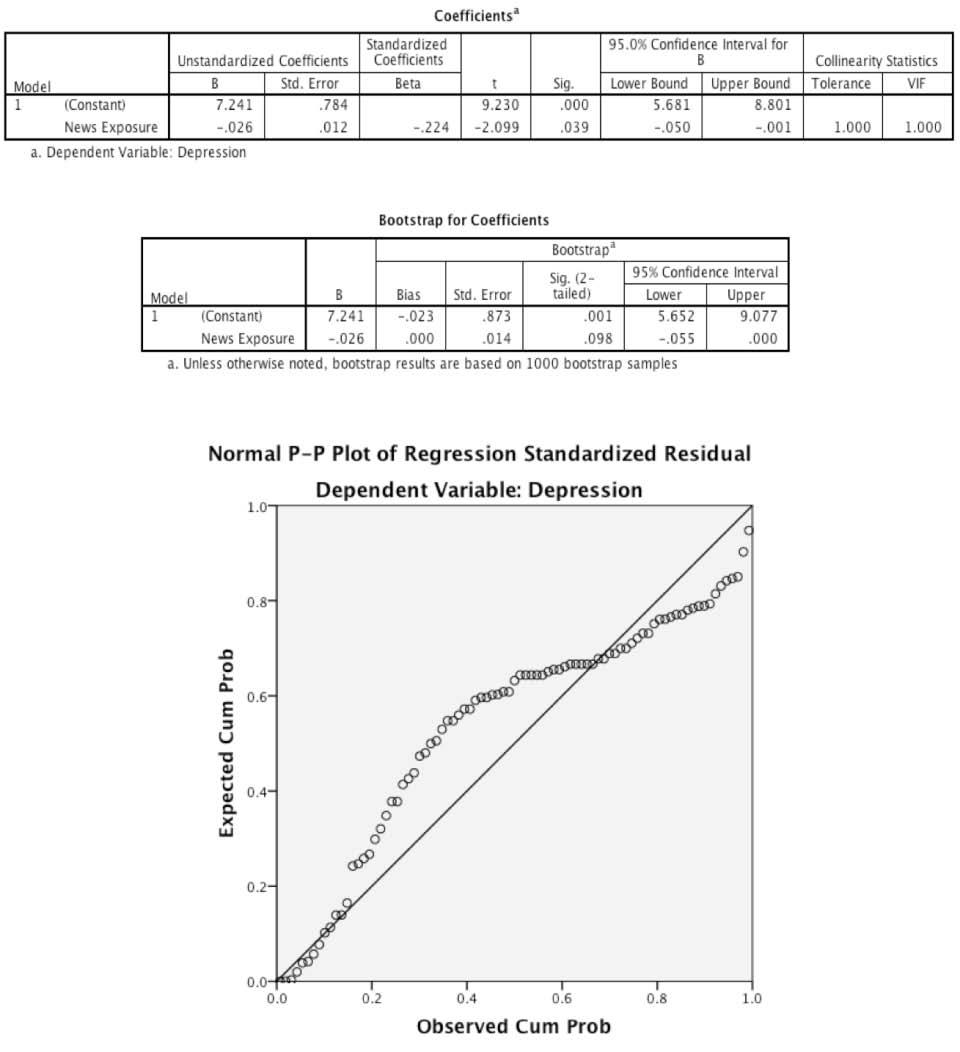
  1. Yes, because the p-value for news exposure is .039, which is less than .05.
  2. No, because the bootstrap confidence interval for news exposure contains zero. 
  3. Yes, because the confidence interval for news exposure does not contains zero.
  4. No, because the b-value for news exposure is close to zero.

The correct answer is b) No, because the bootstrap confidence interval for news exposure contains zero. This is because the P-P plot shows a non-normal distribution, so we use the bootstrapped confidence interval.

5.    A consumer researcher was interested in what factors influence people's fear responses to horror
films. She measured gender (0 = female, 1 = male) and how much a person is prone to believe in things
that are not real (fantasy proneness) on a scale from 0 to 4 (0 = not at all fantasy prone, 4 = very fantasy prone). Fear responses were measured on a scale from 0 (not at all scared) to 15 (the most scared I have ever felt). How much variance (as a percentage) in fear is shared by gender and fantasy proneness in the population?

Ch 14_Fig 5

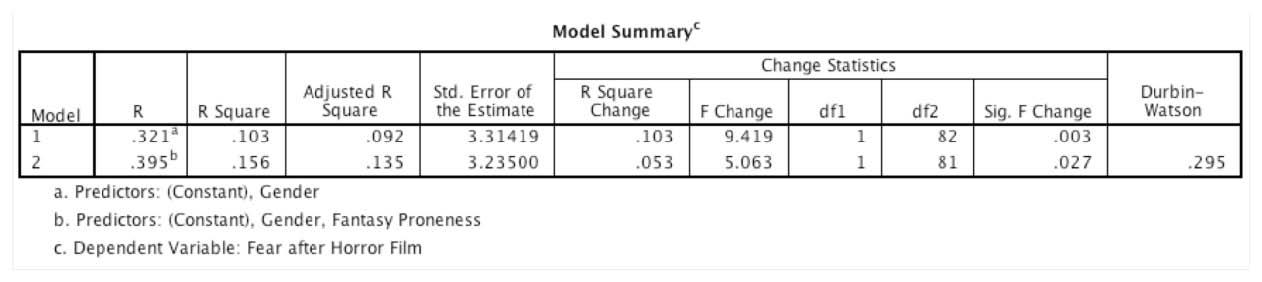
  1. 13.5%
  2. 15.6%
  3. 39.5%
  4. 7.4%

The correct answer is a) 13.5%. This is because the adjusted R2 value tells us how much variance in Y would be accounted for if the model had been derived from the population from which the sample was taken.