Social Statistics for a Diverse Society
Eighth Edition
Chapter Main Points and Learning Objectives
Chapter main points
- A scatter diagram (also called scatterplot) is a quick visual method used to display relationships between two interval-ratio variables.
- Equations for all straight lines have the same general form:
![]()
- The best-fitting regression line is that line where the residual sum of squares, or Σe2, is at a minimum. Such a line is called the least squares line, and the technique that produces this line is called the least squares method.
- The coefficient of determination (r2) and Pearson’s correlation coefficient (r) measure
- how well the regression model fits the data. Pearson’s r indicates the strength of the association between the two variables. The coefficient of determination is a PRE measure, identifying the reduction of error based on the regression model.
- The general form of the multiple regression equation involving two independent variables is
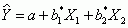 . The multiple coefficient of determination (R2) measures the proportional reduction of error based on the multiple regression model.
. The multiple coefficient of determination (R2) measures the proportional reduction of error based on the multiple regression model. - The standardized multiple regression equation is
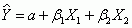 . The beta coefficients allow us to assess the relative strength of all the independent variables.
. The beta coefficients allow us to assess the relative strength of all the independent variables.
Learning objectives
- Describe linear relationships and prediction rules for bivariate and multiple regression models
- Construct and interpret straight-line graphs and best-fitting lines
- Calculate and interpret a and b
- Calculate and interpret the coefficient of determination (r2) and Pearson’s correlation coefficient (r)
- Interpret SPSS multiple regression output
- Test the significance of r2 and R2 using ANOVA
