Discussion Question #1

Select an interval/ratio variable from any of the SPSS modules and discuss the properties associated with its level of measurement. Why do interval/ratio variables retain the properties of nominal and ordinal variables, yet the opposite is not true? What are these properties? Next, as a class or small group, recode this variable. See if you can transform it into an ordinal or nominal level variable. For example, a variable of interest might be annual income measured in U.S. dollars. By simply recoding this variable, we can view income as an ordinal variable measured in dollar intervals (e.g., $20,000–29,999 and $30,000–39,000) or as a nominal variable with two discrete categories (e.g., $25,000 or ~$25,000).^[1]

Discussion Question #2

Are there any research questions or specific hypotheses where it would be advisable to study the entire population, as opposed to just a sample? If so, what characterizes these situations? Which types of research questions and hypotheses lend themselves to a study of the entire population? Which types do not and why?

Discussion Question #3

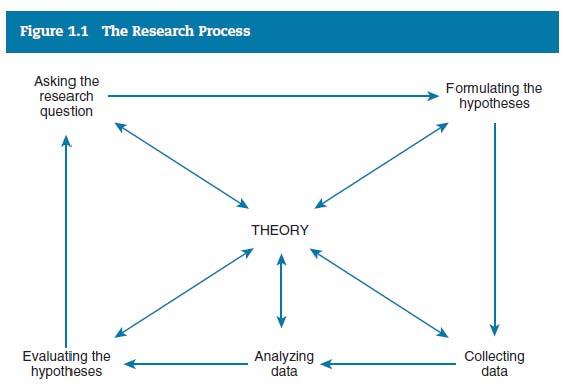
Figure 1.1 in the textbook characterizes the research process as a largely iterative process involving five stages with theory entering in at each. Discuss how theory informs and is informed by:

1. Asking the research question
2. Formulating hypotheses
3. Collecting data
4. Analyzing data
5. Evaluating hypotheses

Does theory affect any of these stages disproportionately? Why or why not?

Discussion Question #1

At the close of Chapter 2, we presented several frequency distributions which provide summary statistics on several economic and social indicators for Mexicans living in the United States. In each of these frequency distributions, only partial information is displayed. Discuss why this is the case. What are the advantages and disadvantages of utilizing different formats when creating frequency distributions? Why would researchers be motivated to use frequency distributions that present only partial information?

Discussion Question #2

Discuss the characteristics of a rate in light of the definition presented in Chapter 2. Describe some specific research problems and/or study designs that are particularly appropriate for the use of rates. Are there any research problems and/or study designs where the use of rates may be inappropriate? Are you satisfied that the risk set (i.e., the population at risk) adequately and concisely captures the risk of exposure to some event? Why or why not?

Discussion Question #3

What is the difference between a bar chart and a histogram? Why are the bars separated in the former but not in the latter? What types of variables are appropriate for each? As a class, discuss a classification scheme for deciding what type of graphic device to use for the following types of variables: discrete, dichotomous, nominal, ordinal, interval/ratio, and continuous. Is there any additional information that would be useful to consider toward helping students to avoid confusing the two?

Discuss Question #4

Which type of chart would we most likely use in a study that examines the rate of AIDS incidence over the past 30 years? What are the reasons for using this type of chart?

Discuss Question #5

How are bar graphs and pie charts used by news correspondents during political elections? How are these graphs and charts useful for conveying or summarizing voting patterns in a brief time span (1–2 seconds)?

Discussion Question #1

Discuss the three properties of the mean as outlined in Chapter 3. Explain how each of these properties is unique to the mean and not to the median or the mode.

Discussion Question #2

What does it mean to have a skewed distribution? What causes a skew in statistical terms? And how does one deal with skewed data when conducting research? Are there specific types of research questions and types of data where one would expect the data to be skewed?

Discussion Question #3

Describe how the wording of survey questions may skew the data. For example, would asking about interest in gender studies courses versus interest in women’s studies courses influence the responses?

Discussion Question #4

Are there any conditions in which it would be acceptable to allow skewed variables into a research study? If so, describe these conditions.

Discussion Question #1

What are the steps involved in calculating the variance and the standard deviation as provided in Chapter 5? Why is it necessary to square the deviation of each observation from the mean? For example, why can’t we just add these values up and use this quantity, , as our measure of variability?

Discussion Question #2

Instructors can provide the class with several scholarly articles that report the means and standard deviations in their tables. Discuss the following questions as a class:

What do these values tell you about the shapes of these distributions? Should the author(s) have reported another measure of central tendency? If so, or if they did, which measure did they report and why?

Discussion Question #3

Instructors can locate an example of box plot and present this to the class. Discuss the following questions as a class:

1. Locate the following measures on the box plot: the median, the range, quartiles, the interquartile range, and the minimum and maximum values.
2. How are the former four calculated?

Discussion Question #4

When summarizing scale variable data using descriptive statistics, what do we lose in our understanding of a sample if we just report the mean and not any measures of dispersion like range or standard deviation?  How does this question apply to a variable like age or test scores?

Discussion Question #1

Imagine that you recently took a statistics exam and your instructor just returned your graded exam. The instructor announces that 75% of students scored below the mean. How do you reconcile this with the fact that, in a normal distribution, half the scores should fall below the mean and half of the scores should fall above the mean?

Discussion Question #2

Compare and contrast an empirical distribution and a normal distribution. Describe the value of each distribution. Discuss the terminology that is invoked to denote the former and the terminology that is invoked to denote the latter.

Discussion Question #3

According to the material presented in Chapter 5, why do researchers use Z scores? What are the advantages of using Z scores? Describe some research questions that would require the use of Z scores. Are there any research questions that would not be appropriate for the use of Z scores?

Discussion Question #4

Why can we NOT assume that for any scale variable, 50% of cases are above the mean and 50% are below the mean?

Discussion Question #5

Why do we use a bell curve to assess the normality of a variable as opposed to a square, triangle, or some other symmetrical shape?

Discussion Question #1

How is a sampling distribution different from the distribution of a sample? From the distribution of a population? What do these differences tell us about the properties of a sampling distribution?

Discussion Question #2

Describe the Central Limit Theorem. How does it help us to move from talking about a particular sample to the population via a sampling distribution?

Discussion Question #3

Compare and contrast the following sampling strategies: simple random sampling, systematic random sampling, and stratified random sampling.

Discussion Question #4

In what situation would we examine a normal distribution curve? In what situation would we examine a sampling distribution curve?

Discussion Questions #5

If we took three different samples of high school students (one from California, one from Nebraska, and one from Alabama) and each sample had 500 students, what would the sampling distribution for age look like? What about for parent’s annual income? What about for number of snow days? Explain each response and draw a distribution curve for each event.

Discussion Question #1

In Chapter 7, estimation is defined as a process whereby we select a random sample from a population and use a sample statistic to estimate a population parameter. As a class, discuss some helpful ways for thinking about estimation. Are there particular terms, examples, or graphics that are useful for remembering this definition?

Discussion Question #2

In the 2016 presidential election, most Americans were inundated with poll results, all of which reported a margin of error. Discuss what a margin of error means for poll results. What does it tell us and why is it necessary to include this information in poll results?

Discussion Question #3

What is the role of sample size in the calculation of confidence intervals? In Chapter 7, we learned that we can increase the precision of a confidence interval by increasing the sample size. Discuss the concept of an ideal sample size. Is there an ideal or optimal sample size? If yes, what is it and how to calculate it? If not, why not?

Discussion Question #4

Discuss the type of situations in which we would want a 95% confidence interval. In what situations would we want a 99% confidence interval?

Question #1

What is the aim of hypothesis testing? What does hypothesis testing achieve that could not be otherwise achieved?

Question #2

What is the distinction between the z and t statistics? Identify the particular quantity that distinguishes these two statistics. Is there a particular class of research questions that lend themselves to testing via the z statistic? If so, what are the characteristics of these questions and data?

Question #3

Discuss the difference between a Type I error and a Type II error. Is it easier to commit one type of error more than another? Is one type of error more detrimental than another? Why or why not?

Question #4

What is the purpose of writing down and testing the null hypothesis?

Question #5

What is the point of doing a hypothesis test if one is given data that show there is a difference between two groups, or that there has been an increase or decrease over time?

Question #6

How does hypothesis testing help support the fields of sociology or political science as sciences that employ the scientific method? Besides hypothesis testing, are there alternative ways to validate the research findings of social scientists?

Question #1

Identify some research situations where the use of bivariate tables is not appropriate. What do these situations have in common and how do researchers deal with them (e.g., by recoding our variables or finding another way to organized our data altogether)?

Question #2

What does it mean to say that the relationship between two variables is “conditioned” by a third variable? What criteria can we use to determine whether or not there is a conditional relationship? As researchers, what do we do once we have determined that there is a conditional relationship? How may this conditional relationship be interpreted?

Question #3

Explain what is meant by a positive relationship between two variables and a negative relationship between two variables. Describe examples of situations in which one would expect to find a positive relationship and when one would expect to find a negative relationship. Can one assign direction when both variables in a table are dichotomous?

Question #1

Discuss how the concept of statistical independence underlies statistical hypothesis testing in general. Based on statistical analysis, are we justified in asserting that two variables are statistically dependent? Why or why not? Explain why researchers typically focus on statistical independence rather than statistical dependence.

Question #2

Does the utility of chi-square decline as we begin to compare variables with more and more groups? For example, imagine we are interested in comparing religious affiliation against political persuasion in the United States. There is a plethora of categories designed to capture information about each variable of interest. How useful is chi-square in telling us anything substantive about the relationship between these two variables?

Question #3

Suppose you were using the percentage difference method to determine the relationship between two variables of interest arranged in a bivariate table. Are there any instances where you might find a very large percentage difference yet fail to find statistically significant results after conducting a chi-square test? If so, what factors would explain this?

Question #4

What are we calculating when we calculate expected frequencies? What is the reason for calculating expected frequencies the way we do? In laymen’s terms, what do expected frequencies tell us?

Question #5

Contrast and contrast symmetrical and asymmetrical measures. Is it generally good practice to rely on symmetrical measures of association? Why or why not?

Question #6

The calculation of gamma relies on the comparison of same-ordered and inverse-ordered pairs. The calculation of tau-b relies on the additional concept of tied pairs. What is a tied pair? How do such pairs differ from same-ordered and inverse-ordered pairs? Which of these measures is preferable and why?

Question #7

When conducting chi-square analyses, what do we gain from reporting PRE measures or from discussing the strength of significant relationships? Discuss an example in which it would be important to report not only significance but also strength.

Question #1

How is ANOVA different from linear and multiple regression? What are the steps in the former compared to the steps in the latter? Are there some problems that tend themselves to an ANOVA framework and some that do not? Provide a few examples and discuss these as a class.

Question #2

The two-sample t-test is useful because it compares the means between two groups, whereas ANOVA compares the means across multiple groups (e.g., Republicans, Democrats, and Independents). Does the utility of ANOVA decline as we begin to compare more and more groups?

Question #3

Describe the F-statistic, or the F-ratio, as discussed in the chapter. As a ratio, what is the numerator and what is the denominator?

Question #4

Based on either your own research or research you have read about in the literature, which hypothesis test is the most common? What are some reasons why this test may be more common than others?

Question #5

Discuss why we use two degrees of freedom values to find critical F in ANOVA.

Question #1

What is the difference between Pearson’s correlation coefficient, r, and the coefficient of determination, r²? What does each statistic tell us about the relationship between two variables? What do these statistics NOT tell us about the relationship between two variables?

Question #2

Discuss the reasons and situations in which researchers would want to use linear regression. How would a researcher know whether linear regression was the appropriate statistical technique to use? What are some of the benefits of fitting the relationship between two variables to an equation for a straight line?

Question #3

What is the difference between strength and fit when interpreting regression equations? Do we always need to report and discuss both?

Question # 4

When reporting Pearson’s R, do we always have to report R² along with it? Why or why not?